5주차 ML 지도학습 WIL
ml3 비지도학습과 데이터 전처리
비지도 학습이란 ?
알고 있는 출력값이나 정보 없이 학습 알고리즘을 가르치는 머신러닝
3.1 비지도 학습의 종류
비지도 변환 : 데이터를 새로 표현하여 원래보다 쉽게 해석할 수 있도록 만든 알고리즘
ex) 차원 축소
군집 알고리즘 : 데이터를 비슷한 것끼리 그룹으로 묶는 것
ex) 텍스트 문서에서 주제 추출
3.2 비지도 학습의 도전 과제
비지도 학습은 잘 하고 있는지 확인하기가 어려움 ! (직접 확인하는 수 밖에..)
이런 이유로 데이터를 잘 이해하고 싶을 때, 탐색적 단계에서 많이 사용
또한 지도 학습의 전처리 단계에서도 사용 (지도 학습에 사용되지만 지도 정보를 사용하지 않으므로 비지도 학습)
3.3 데이터 전처리와 스케일 조정
3.3.1 여러 가지 전처리 방법
StandardScaler : 고등학교 수학 시간에 배운 표준화를 통해 각 데이터의 표준값(z). 최댓값과 최솟값의 제한 없음.
MinMaxScaler : 데이터에서 최솟값 빼고 전체 범위로 나눔. 최솟값이 0, 최댓값이 1, 나머지는 그 사이 (지난 시간에 잠깐 나옴)
RobustScaler : StandardScaler 에서 평균과 분산 대신 중간값과 사분위값을 사용. 이로 인해 이상치에 영향을 받지 않음.
Normalizer : 특성 벡터의 유클리디안 길이(l2)가 1이 되도록 데이터 포인트를 조정. 길이가 다 같아지고 방향만 남게 됨.
3.3.2 데이터 변환 적용하기
데이터 변환을 적용할 때, 테스트 세트에서도 훈련 세트의 최솟값(평균, 중간값 등)을 빼고 훈련 세트의 범위(분산 등)로 나눠야 합니다.
따라서 MinMaxScaler의 경우, 테스트 세트에서는 범위의 최댓값과 최솟값이 각각 1과 0을 넘어갈 수 있습니다.
3.3.3 (한국어판 부록) Quantile Transformer와 PowerTransformer
Quantile Transformer
scikit-learn 0.19.0 버전에 추가되었고, 기본적으로 1000개의 분위를 사용하여 데이터를 균등하게 분포시킵니다.
이상치에 민감하지 않고, 값을 0과 1사이로 압축
Power Transformer
scikit-learn 0.20.0 버전에 추가되었고, 데이터의 특성별로 정규분포 형태에 가깝도록 변환해줍니다.
실전에서는 데이터셋마다 어떤 변환이 정규분포에 가깝게 변환할지 미리 알기 어렵기 때문에 히스토그램을 통해 확인해보자 !
3.3.4 훈련 데이터와 테스트 데이터의 스케일을 같은 방법으로 조정하기
위에 말한 것과 같이 테스트 세트에서도 훈련 세트의 값들을 사용해야 합니다.
그렇지 않을 경우, 아래의 그림과 같이 배열이 뒤죽박죽으로 섞이게 됩니다.
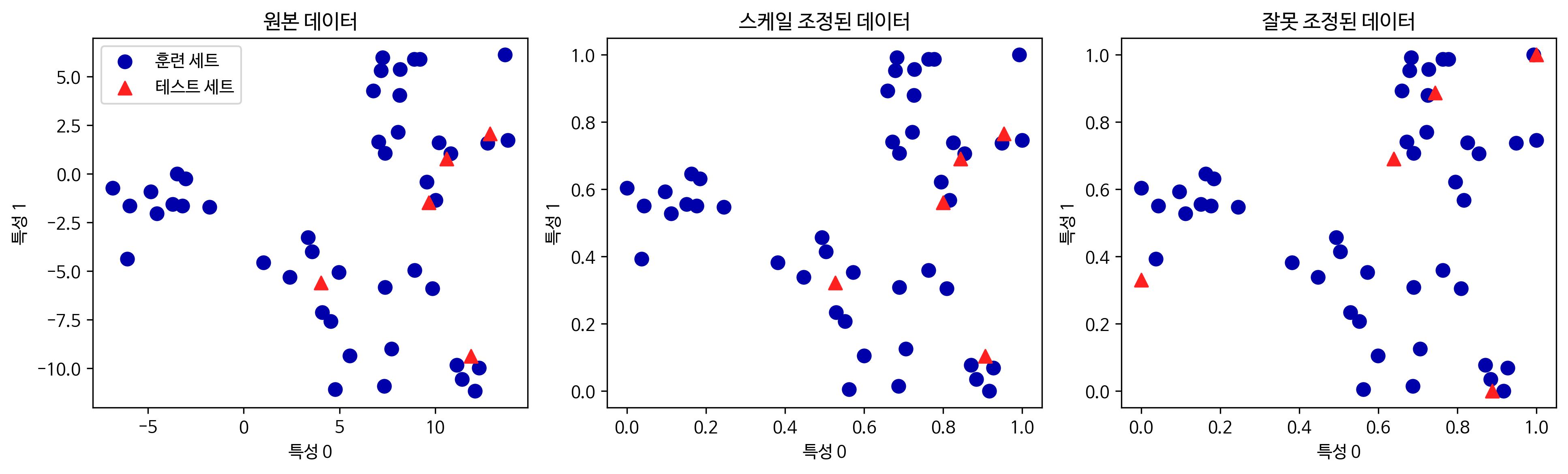
3.3.5 지도 학습에서 데이터 전처리 효과
지난 시간에 배운 것과 같이 간단한(?) 전처리로 성능이 크게 향상되는 것을 알 수 있습니다.
기존 정확도 0.63 -> MinMaxScaler와 StandardScaler로 스케일이 조정된 정확도 0.95, 0.97
3.4 차원 축소, 특성 추출, 매니폴드 학습
3.4.1 주성분 분석(Principal Compnent Analysis)
주성분 분석은 특성들이 통계적으로 상관관계가 없도록 데이터셋을 회전시키는 기술
회전한 뒤에 데이터를 설명하는데 얼마나 중요하냐에 따라 종종 일부만 선택(이 때, 차원 축소)됩니다.
우선 분산이 가장 큰(가장 넓~게 분포된, 범위가 넓은(?)) 방향을 찾고 이 방향과 직각인 방향을 찾습니다.(2차원에서는 그 방향이 하나이지만, 고차원에서는 무수히 많음)
이렇게 찾은 방향들이 주성분(principal component) 입니다.
PCA를 적용해 유방암 데이터셋 시각화하기
PCA가 가장 널리 사용되는 분야는 고차원 데이터셋의 시각화
PCA의 단점은 모든 feature들의 영향이 조금씩 섞여있기 때문에 그래프의 축을 해석하기가 쉽지 않다는 것
고유얼굴 특성 추출 (어려움 ..)
PCA는 특성 추출에도 사용
특성 추출은 원본 데이터 표현보다 분석하기에 더 적합한 표현을 찾을 수 있으리란 생각에서 출발
얼굴의 유사도를 측정하기 위해 원본 픽셀을 사용하는 것은 한 픽셀만 달라도 큰 차이가 되어 좋지 않은 방법
그래서 주성분으로 변환하여 계산 *화이트닝을 사용하면 주성분의 스케일이 같아지도록 조정(StandardScaler를 적용하는 것과 같다)
이후 학습을 통해 주성분을 출력하면, 아래의 사진과 같이 출력됩니다.
첫번째 주성분은 얼굴과 배경의 명암 차이를 기록한 것으로 보인다고 하는데 잘은 모르겠습니다.
확실한 것은 사람의 방식과는 다르다는 점입니다.

아래의 사진은 테스트 이미지를 주성분의 가중치 합으로 분해한 PCA 구성도 입니다.
즉 각각의 주성분 앞에 붙은 계수가 어떻게 곱해지냐에 따라 다른 사람의 얼굴이 나오는 것입니다.

PCA를 이용하는 또 다른 방법은 아래의 사진과 같이 일부의 주성분만을 사용해가며 원본 데이터를 재구성하는 것입니다.
아래의 그림은 10, 50, 100, 500개를 사용한 것인데, 점점 많은 성분을 사용할수록 이미지가 상세해집니다.
즉, 위의 사진에서 주성분과 주성분의 계수를 계속해서 더하는 것과 같습니다.
원본의 픽셀인 5,655 차원에서 10, 50, 100, 500개의 차원으로 변환한 형태이기 때문에,
주성분과 주성분의 계수를 5,655까지 더하게 되면 결국 원래의 이미지와 완벽하게 동일한 이미지가 출력됩니다.

마무리
과제가 많아 힘든 한 주였지만, 동시에 얻어간 것도 많은 뿌듯한 한 주였던 것 같습니다.
그리고 PCA가 좀 어려웠는데 내일 있는 세션 전까지 조금 더 공부를 해봐야 할 것 같습니다.


